1.2 基本地理作用
1.2.1 流体作用
地球表层很多现象是流体现象或者与流体运动有关.常见的坡面水流过程与水土流失是流体运动现象,大气圈是由“流体”构成的.流体的观念还被推广到人口空间运动、城市空间发展等地理现象中.本节内容,不在于讨论这种观念的合理性,读者会在本书以后的内容中体会到这种合理性.本节和下节的目的在于为那些不太熟悉流体力学、统计力学、系统论的读者提供一个必要的阅读基础和从地学角度讨论某些概念的意义.
流体就是易变形的可能流动的连续介质,它与固体的差别在于固体能够抵抗一定的拉力、压力和剪切力.在一定外力作用下,固体能产生变形以抵抗外力的作用,从而达到某种平衡状态,一旦释去外力,这种变形部分是能恢复的;流体则不同,在任何微小切应力的持续作用下它将连续地变形,释去外力,不可能恢复原状.流体与固体的过渡状态称为流变体.流体现象、固体现象、流变体现象在地理空间(地球表层空间)都是常见的,都参与塑造地理事物,但流体现象更具有地理意义.真实的流体具有可压缩性、粘性(抵抗剪切变形的一种属性)、导热性、扩散性(由于分子运动引起)等,在地理学分析的不同场合,分别忽视某些性质.一般的流体力学方程由连续性方程和运动方程构成.在某一时刻t,空间点x上的流体速度V满足

式中,V为流体速度,ρ为流体密度,P为流体的应力张量,F为作用于单位质量流体上的质量力分布,ρF为单位体积流体所受的质量力.这一方程组描述了没有质量交换的流体的力学运动,其中算子D/Dt为全微分算子,div为散度算子,即
![]()
这里,grad为梯度算子,rot为旋度算子.在许多情况下,还需要考虑流体的热力学过程或者说能量平衡,因为这类过程中热力变化具重要意义.这时需引用能量方程

(1.2.4)
式中,U为单位质量的内能,T为流体温度,q为传入单位质量的热分布函数,k为热传导系数.式(1.2.1),(1.2.2),(1.2.4)是较复杂的,一般的地理分析中采用忽视某些流体性(如粘性、可压缩性等)的流体方程,地理学中常用的是欧拉(Euler)方程,它对理想流体(无粘性流体)成立
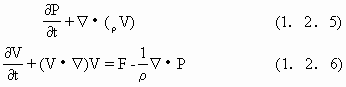
式(1.2.5)就是式(1.2.1),式(1.2.6)是式(1.2.2)的简化,其中对应应力张量的项在直角坐标系中为

(1.2.6)式在xyz空间实际上为三个方程.如果将(1.2.6)式简化为
![]()
则称纳维埃-斯托克斯(Navier-Stokes)方程或简称N-S方程.方程(1.2.1)到(1.2.8)的推导过程可见吴望一(1982,PP.145—161).在地理学中,一般流体常被考虑为具有有限层厚的受重力作用的流体,这时方程(1.2.5),(1.2.6)可以代之以浅水方程

式中u,v分别为沿x,y方向的断面平均速度,H为流体上界面高程,h为流体厚度,τxb和τyb分别为流体层界面上沿x方向和y方向的切
![]()
![]()
时为切应τxz,τyz,其导出过程的关键为沿断面求平均流速,详细步骤可参见简森,1979,中译本,1986,PP30—32.当考虑粘滞作用时
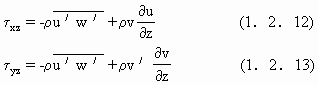
式中,v为运动粘滞系数.在海洋环境中还必须考虑科里奥利(Coriolis)力的作用

式中,f为科里奥利力因子,取值为2ωsinθ,这里ω为地球自转角速度,θ为纬度,其导出过程可参见Pedlosky(1979,PP.58—63).
![]()
![]()
或者说

在二维通常不可压缩流动的情况下,由连续方程容易发现,φ满足拉普拉斯(Laplace)方程
![]()
流函数ψ定义作

连续方程化作
![]()
N-S方程化作
![]()
![]()
认为粘滞力远大于惯性力,这时有
![]()
这是一个线性方程,它对于蠕动现象是适合的.
仅有最基本的流体力学方程求某些实际问题是不充分的,因为连续介质可能还会发生状态变化,因此必要时要补充状态方程.其次参数v,k还可能因状态(温度)发生变化而变化在应力作用下,物质对力有某种响应关系,这种关系称作本构关系①,如应力与变形的线性关系.地理学中最常用的本构关系是边界层关系
![]()
![]()
度,容易看出μ是流体抗拒变形的内摩擦的量度.在地理学中(1.2.26)式被常用于分析上层流动时下层流体或流体的拖曳作用.总之流体力学基本方程包括连续性方程(1.2.1)、运动方程(1.2.2)、能量方程(1.2.4)和联系应力与变形的本构方程和联系温度与压力的状态方程.在地理学分析中,常常考虑流体对泥沙的搬运作用,这时还需补充泥沙连续性方程和流速与输沙率的关系等.以后,我们将会熟悉这些情况.在不严格的情况也可由某些经验公式代替运动方程.在求解实际问题时,如果不涉及状态变化,一般仅需方程(1.2.1),(1.2.2)和相互作用关系.为方便本书将相互作用关系、状态关系等统称作结构关系.
流体模式一般适合于地球表层真实流体及其产生的景观过程分析.多年来它也被用于分析人口在连续背景空间的运动,这时只能是种学说.
1.2.2 随机过程模式与粒子作用
连续介质模式或流体过程模式,一般描述的是具有确定性过程的地理现象.在地理学中,由于对象的中观性,许多现象很难从运动本原上说明,而且我们关心的也不是个别单元的运动而且它们的统计规律,这就引出将地理过程看作是随机过程或受到随机干扰的观点.地理状态是随机的,地理系统受到随机因子作用.与之配合的是地理单元.如人口、泥沙可以看作大量粒子组成的总体,有地理意义的是它们微观(个别)运动产生的宏观总体运动分布,即它们运动是随机的,景观是它们微观状态的最可能分布对应的某些宏观可测量,如人口的空间分布、人口迁移法则、区位分导等.
为了研究地理粒子运动和一般随机地理现象,假设地理事物的状态构成状态空间,在t时刻它的状态为x(t),x(t)是随机变量,x(t)可以是n维的.随着t的演变,随机变量x(t)也演变,在某一时刻t0,x(t0)服从确定的概率分布,粒子的状态x(t)就被称作随机过程.实际上,t定义于集合T内,T内有无穷个t({…,-3,-2,-1,0,1,2,3,…},或[a,b]),所以也就有x(t)对应的无穷个随机分布,x(t1),x(t2),x(t3),(离散时)…,分开来看又是无穷多个相互有关的随机变量,称它们为一簇.对应的分布函数称为x(t)的分布函数族.如果这种分布与时间无关,而且x(tj)的分布函数不与x(ti)有关系,则知随机过程为具有独立同分布的随机过程.当T为离散集时,x(t)取“时间”离散的值,称随机序列.如果允许的x(t)的状态是有限的,即x(t)只能取有限个值,则称{x(t),t∈T}为有限状态随机过程.有限状态随机过程在地理学中是常见的.例如泥沙运动可能的状态是静止、滚动、跳动、浮悬,泥沙状态x(t)只有四种,人口运动也常被取作在城市与农村中的运动,只有两种状态,是二值随机过程,后者往往具有很好的数学理论与模型.
数学上严格地描述了随机过程.设{X(t),t∈T}是个随机过程,为描述它的统计特性,我们要知道每个t∈T的X(t)的分布函数
![]()
我们称F(t;x)为随机过程{X(t),t∈T}的一维分布或样本函数,并且定义
m(t)≡E{X(t)}
(1.2.28)
D(t)≡E{(X(t)-m(t))2}
(1.2.29)
当(1.2.28),(1.2.29)右端存在时分别称m(t),D(t)为随机过程{X(t),t∈T}的均值函数和方差函数.仅有一维分布还不足于描述随机过程,随机过程不同时刻x(t1),x(t2),x(t3),…之间可能存在某种关系,为此需要引入高维分布,特别是两个随机变量之间的关系颇受重视,定义随机过程{X(t),t∈T}的二维分布为
F(t1,t2;x1,x2)≡P{X(t1)<x1,X(t2)<x2},t1,t2∈T
(1.2.30)
其中t1,t2是不同时刻,类似地有n维分布.对于二维分布可引入协方差函数
B(s,t)=cov{X(s),X(t)}=E{X(s)-m(s)(X(t)-m(t))}
(1.2.31)
随机过程{X(t),t∈T}的一维分布,二维分布,…,n维分布,其全体{F(t1,t2,…,tn;x1,x2,…,xn,t1,t2,…,tn∈T;1≤n<∞},称为随机过程{X(t),t∈T}的有限维分布函数族.如果知道了随机过程{X(t),t∈T}的n维分布全体,也就知道了这个随机过程.
随机过程有多种类型,地理学中常见的是布朗运动.马尔科夫过程和平稳过程.布朗运动是布朗观察悬浮在液体中花粉微粒时发现的,这种粒子在空间作无规则运动,爱因斯坦在1905年求出了这种粒子的转移密度,维纳(Wiener)1923年从数学上严格定义了布朗运动,因此布朗运动的增量也被称作维纳过程.布朗运动X具有四个基本性质:1)X(0)=0;2)独立增量性,即对任意的0≤t0<t1<…<tn,X(t0),X(t1)-X(t0),X(t2)-X(t1),…,X(tn)-X(tn-1)是相互独立的随机变量;3)对于任意s≥0,t>0,增量X(s+t)-X(s)服从n维正态分布(当x是n维的);4)X的一切样本函数连续.
布朗运动实际上仅是一种重要的随机过程——马尔可夫过程的特例.当状态随机过程为{X(n),n=0,1,2,…}时,马尔可夫过程又称为马尔可夫链;当X(n)是离散的,为离散状态马尔可夫链,这种模型在地理学中应用颇多.对于马尔可夫链来说,它具有如下性质:若对任意非负整数t1<t2<…<tr<t,只要
P{X(t1)=i1,X(t2)=i2,…,X(tr)=ir}>0
(1.2.32)
就有
P{X(t)=j|X(t1)=i1,X(t2)=i2,…,X(tr)
=ir}=P{X(t)=j|X(tr)=ir}
(1.2.33)
这个性质称马尔可夫性或无后效性,它的物理意义是:“未来”状态X(t)仅与“现在”状态X(tr)有关而与过去状态{X(t1),X(t2),…}“无关”(严格地讲是由“现在”的信息即可推断“未来”状态,无需过去信息,或者说在“现在”已知的条件下,“未来”的状态与“过去”无关).对于马尔可夫链来说,描述它概率性质最重要的数学形式是它在时刻r的一步转移概率
pij(r)=P{X(r+1)=j|X(r0)=i}i,j∈I
(1.2.34)
这里I为状态集;显然pij(r)有下列性质
pij(r)≥0 i,j∈I
(1.2.35)
![]()
(1.2.36)式的意义是状态转移总归是转向状态集合中的某一状态.类似地可以定义r时刻的k步转移概率
![]()
(1.2.37)
它也有类似于(1.2.35),(1.2.36)式的性质和物理解释.而且通常规定
![]()
这里δij具有性质:δij=0(i≠j),δij=1(i=j).对于状态转移概率有切普
曼-柯尔莫哥洛夫(Chapman-KомиогороB)方程成立
![]()
(1.2.38)
这一关系的物理意义是不难解释的.在状态转移概率基础上进一步可以
![]()
式可写成简洁的矩阵形式
P(k+l)(r)=P(k)(r)P(l)(r+k)
(1.2.39)
对于连续的随机过程{X(t),t∈T}来说,如果对任意的t1<t2…<tn及ti∈T,X(tn)关于X(t1),X(t2),…,X(tn-1)的条件分布恰好等于X(tn)关于X(tn-1)的条件分布,即
P{X(tn)<y|X(tn-1)=xn-1,…,X(t1)=x1}
=P{X(tn)<y|X(tn-1)=xn-1}
(1.2.40)
成立,则称过程{X(t),t∈T}为马尔可夫过程.马尔可夫过程可能取值的全体,定义了它的状态空间.马尔可夫过程
P(s,x;t,A)=P(x(t)∈A|x(s)=x}
它的意义是当时刻s时,状态为x的过程或系统的时刻t状态转移到状态子集A的(条件)概率.特别当A=(-∞,y)时有
P[s,x;t,(-∞,y)]≡F(s,x;t,y)=P{X(t)<y|X(s)=x}
(1.2.41)
式中,F(s,x;t,y)称作转移概率分布.它是关于y的一个分布函数,因此有F(s,x;t,y)≥0,F(s,x;t,∞)=1,F(s,x;t,y)关于y单调不减左连续,它的导数
![]()
(1.2.42)
为马尔可夫过程的转移(概率)密度,这是最常用的概率.在某一些特殊的场合,F(s,x;t,y)只依赖于t-s,而不直接依赖于s,t本身,这时F(t-s;x;y)=F(s,x;t,y),称为{X(t),t∈I}齐次马尔可夫过程.类似的有齐次马尔可夫链,即对于任意两个m和n时刻的两个状态i和j来说,只要p(X(n)=i)>0,p(X(m)=i)>0,则有
p[X(n+r)=j|X(n)=i]=p[X(m+r)=j|X(m)=i].
独立同分布的随机序列{X(n)},必定是齐次的.
平稳随机过程适合于另一类重要的地理过程.如果复随机过程(X(t),t∈T}具有有限的二阶矩阵,即E|X(t)|2<∞,并且满足

则称{X(t),t∈T}为平稳随机过程,或平稳过程.当T为整数集(离散集)时,称{X(n),n=0,1,…}为平稳时间序列.平稳过程的协方差函数
![]()
平稳随机过程的一个重要特点是它可以作谱分解,即认为它是由无穷个特定频率的振动序列合成的.白噪声是一种重要的随机过程,它包括各种频率的振动,它的协方差为0.许多地理学分析中,假定地理过程或状态序列是平衡过程(或者它们的增量是平稳过程).例如气候的周期分析,遥感图像分析.由于地球表层系统的单向演化性,只能认为在局部时段或地段(1.2.43),(1.2.44)才成立,即可设地理现象是平稳随机过程.事实上从全球看,地带性递变是单向的,故不是平稳的.但一个区域内,山地的地带谱也具有重复性,可以认为具有某种“平稳性”.总之,在球观问题中,不能引用平衡性假设,在环境演化尺度上,也不能引用这一假定.或者我们约定,凡满足平稳性的地理现象变异为变化,不满足的并且具有某种单向性序列的为演化.这可能有利于地理信号分析.
跳过程是近年来颇受重视的随机过程.设E={0,1,2,…},称E×E上的{X(t),t∈T}的状态转移矩阵P(t)=(pij(t):i,j∈E)(t≥0)为跳过程,如果pij(t)
pij(t)≥0 i,j∈E,t≥0
(1.2.46)
![]()
![]()
![]()
这里的(1.2.46),(1.2.48)式就是(1.2.35)和切普曼-柯尔莫哥洛夫方程.对一切i∈E,(1.2.48)式中等号成立,则称随机过程{X(t),t∈T}是不断的,不然是中断的.对于跳过程来说,可以证明下式定义的转移概率密度
![]()
(1.2.50)
总存在,而且满足
![]()
(1.2.51)
我们称满足(51)式的矩阵Q=(qij:i,j∈E)为Q矩阵,因此跳过程也称Q过程.这里t↓0,t↑0分别表示t→0+,t→0-.
粒子过程的理论是随机过程的基础上展开的.设地理粒子的状态为x,不妨将x看作地理粒子的空间位置,对大量粒子来说,有地理意义的是它们在x∈X的空间上产生的分布u(x,t).u(x,t)就是地理景观.对于个别粒子来说,它受到确定性力的作用,则产生a(x,t)的速度,同时又受到随机干扰,产生b(x,t)的迁移.于是有此时间内粒子的状态迁移(位移)为
dx=a(x,t)dt+b(x,t)dW
(1.2.52)
这W是布朗运动.a(x,t),b(x,t)分别称为偏移系数和迁移系数,分别表示了状态的确定性偏移和围绕t时刻的期望位置的随机偏移.可以证明,求(1.2.52)定义的状态x的概率转移密度函数p(x,t;y,s)满足福克-普朗克方程(Fokker-Planck)也称前向柯尔哥莫洛夫方程
![]()
(1.2.53)
系数b2(y,s)称作扩散系数.我们还有后向柯尔莫哥洛夫方程
![]()
(1.2.54)
其中u(x,t)是(1.2.52)式定义的状态x关于转移概率密度的数学期望
![]()
(1.2.55)
![]()
在高维时,x=(x1,…,xn)τ,W(t)=(w1,…,wn)τ,A=(a1,…,an)τ,B=(b1,…,bn)τ.福克-普朗克方程为
![]()
(1.2.57)
作为一个例子,考虑具有一个吸收壁的布朗运动.对于在x>0上定义且在x=0处是右吸收边界的布朗运动,这时a=0,并取b=1,有福克-普朗克方程
![]()
p(0,t,y)=0 t>0,y>0
(1.2.58)
当t↓0,p(0,t,y)→δ(x-y),x>0,y>0 有初边值解
![]()
(1.2.59)
当a(x,t)=a(t),b(x,t)=b(t)时,可以证明

(1.2.60)
一种重要的随机过程是遍历的或称各态历经.它的特点是:①大量粒子在某一时刻的平均状态或分布的数学期望等于个别粒子在时间趋于无穷时所历经状态的数学期望;②大量粒子状态的方差也等于个别粒子所历经状态的方差.换言之,粒子将历经可能的所有状态而且维持与系统同样的概率性质.对各态历经系统来说,福克-普朗克方程可写作
![]()
(1.2.61)
式中,P(x,t)为粒子的概率(分布)密度阵,它设t=0时,x=0.不然P(x,t)可代以ρ(x-x0,t),x0为初始态.一般的扩散过程满足(1.2.61)式;扩散现象是地理过程中最常见的现象.扩散过程是一种特殊的马尔可夫过程,(1.2.61)描述的扩散过程包含了中心迁移作用a(x,t)和扩散作用b2(x,t).我们可能用它描述城市的发展,它包括了城市中心偏移和地域扩散两种效性.在物理学中,扩散运动被理解为微观上粒子的空间运动,由此可见扩散产了扩张与中心偏移,后者是宏观现象,扩散指的是微观机制,二者不可混淆.
更一般的粒子过程满足主方程,它实际上是由切普曼-柯尔莫哥洛夫方程导出的[参见L.Reichi,雷克,1980,中译本(上),1983,pp166—171],因此它描述的是马氏过程
![]()
(1.2.62)
式中,P为概率密度,W(x,y)为从x转移y的概率转移密度.它表明粒子概率密度P(y,t)的改变由两项组成,从所有其他态x转移到态y和从态y转向所有其他态,它的物理意义是明瞭的.当y的改变以无限小的方式进行,它化作(61)式的福克-普朗克方程.当状态离散,在一个时刻只能进行一步转移时,主方程为

(1.2.63)
这个方程描述了生灭过程,其中λ为单位时间内粒子出生的概率,μ为单位时间内粒子死亡的概率,n为粒子数,P(n,t)为t时刻粒子数为n的概率(阵),n为确定状态,状态n只能转移为n-1或n+1.所以(1.2.63)得以简化.
对于地理粒子来说,很大的一类粒子象人口,寿命有限,本书称其为口或口粒子.对口来说必须作寿命修正,一种近似的方法是将(1.2.61),(1.2.62)求出的密度函数乘上因子
![]()
这一修正的想法是设粒子在(t,t+dτ)内死亡的概率密度为k(τ,x(τ))dτ+0(dτ),于是时刻t存活的概率为(1-μ(x(τ1),τ1)dτ(1-(x(τ2)dτ2)…(1-μ(xn)τndτ)+0(1),当dτ=τj+1-τj→0,即有(1.2.64)式成立.当然在多数情况下,这种修正是近似的.
粒子总体构成了粒子系统,它是具有统计特征,这方面的模式,我们将在下节讨论.
近来发现流体或连续介质中的位势与粒子的随机运动有特定的联系,或者说发现了位势与随机过程之间的关系.这就意味着我们可能从微观的人口迁移、种群扩散、泥沙运动来推求宏观的、域观的空间景观演变趋势.实际上(1.2.61)式的P(x(t))与时间无关,则(1.2.61)化作抛物线型方程,(1.2.58)式则对应于拉普拉斯方程,它的解意味形成一种空间“位势”.理论上最简单的运动是布朗运动与牛顿位势的联系.对于布朗运动,转移概率密度P(t,x,y)与牛顿势有下列联系

(1.2.65)
式中x,y表示空间位置(状态).(65)式表明由布朗运动粒子传递的相互作用,在大于二维的空间,产生以|x-y|2-n形式衰减的势.这里Cn取
![]()
二维空间的布朗运动,以(1.2.65)式定义的位势不合理,在某些假定下,结果发现,存在另一势核,k(x,y),它具有对数形式。π-1log|x-y|.这里求出的位势是对粒子寿命无限长而言的,如果寿命有限,则可能使相互作用衰减得更快,从而产生别的形式的势,如指数势(参见第六章).关于位势的定义与随机过程理论可参见王梓坤(1983).
1.2.3 流作用与热力学作用
在地理学中,能量流、物质流的作用一直受到重视,许多理论建立在这种流(过程)模式基础上.地理世界的流是由流体过程、扩散过程及一般的粒子过程产生的.但它作为一种传递现象又具有统一的理论模式.
流的特点是流的强度与热力学力有一定的关系,流Jm
![]()
这里Xk是第k种热力学力,Jm是第m种流,如质量流、动量流、重力、速度梯度[力]等.αm,k称作唯象系数,“唯象”一词指我们不(必)去理解流与力的微观(机理)过程.在微观的观察下αm,k是随机过程,但在关于流与力的宏观观察下,αm,k是确定的.当αm,k与Xk无关时,(1.2.66)是线性的.这时定义了线性近平衡点的热力学系统,并有αk,m=αm,k成立.当αm,k与Xk有关时,(1.2.66)式是非线性的.非线性的流与力的关系定义了非线性热力学系统,它可能产生耗散结构,因此倍受青睐.然而没有理由认为线性流过程并不重要.
对于具有线性的流与力关系的热力学系统来说,它有一个重要的状态就是平衡态.达到平衡态时系统的宏观可测特征量具有稳定均匀的值.达到这种平衡态的条件是系统是孤立的.对一个热力学系统来说定义一个状态量熵,当系统孤立时,熵趋于最大,这已经是一种科学常识.普里高津(Prigogine)发展的非平衡热力学认为,在远离平衡态附近时系统可能有新的动力学平衡点,使系统达到某种动态的稳态.一个系统所处的暂时平衡状态是否稳定取决于它所定义的超熵生产.
![]()
![]()
系统处于新的非平衡点的稳定,并不具有均匀的性质(特征量),被称之为耗散结构.耗散结构理论,为我们提供了新的思想,同时只要知道在某平衡点附近流与力的关系,我们就由(1.2.67)判断这个平衡点是否稳定.这一方法并不要求特别地建立状态的动力学关系,而是基于物理上可能估计的流与力的关系.
在流与热力学的分析中,有一个重要假定——局部平衡原理,它认为在系统的一个充分小的区域内,我们所关心的状态特征量是平衡的值.显然这个局域与给定的观察有关,比如我们考虑城市间人口迁移时,城市就是局域,考虑市内人口迁移时,街区就是局域,局域内的迁移,如从二楼搬到三楼,对给定的观察没有意义.所以在热力学模式分析中,必须确定最小的,不可分的性质均匀的“局域”.
流作用过程还遵守一系列的平恒律,它们包括质量守恒、动量守恒、能量守恒和熵平衡等条件,这些守恒律导致了流满足
![]()
式中ρ(x,t)为某种量的空间密度,j为对应的流,σ为源强,即在x点t时刻有某种量产生(σ>0)或消失(σ<0).
对于熵来说,它不是守恒量,所以σ不等于零,而对其它守恒量说,一般情况下我们考虑有资源消耗,即σ<0,或者认为无消耗而取σ=0.
这里应该指出,地理系统是开放系统,因此随机干扰的普遍存在,导致了所有地理流过程都是不可逆的.
1.2.4 经济作用
经济作用是地理过程的一个重要的基本动力.经济作用过程可分为宏观经济过程和微观经济过程,宏观经济过程是整个社会的经济结构演变及其行为的过程.宏观经济学把家庭、企业、政府作为三个并行单位,通过分析信贷、投资、产出、就业、全面价格等基本概念来进行社会经济分析.微观经济过程是社会的各经济细胞的经济行为和经济作用,它通过市场结构来集中表现自己.微观经济学就是以个别企业、消费集团等为基本单位,研究经济过程的.无论宏观经济过程和微观经济过程,供给与需求是经济过程的主要矛盾,特别对地理过程来说;但是,不能把宏观经济学和微观经济学的全部问题都归结为地理问题.地理学的经济作用,主要是地区内部、地区与地区之间的经济相互作用.在考虑地区内部的信贷与产出问题时,属于宏观经济学问题;在处理地区与地区空间竞争时,反而可化为微观经济学问题.宏观与微观不是由空间尺度确定的,而是由经济的研究单位结构决定.本文不可能介绍宏观经济学和微观经济学的丰富内容,我们假定读者已经了解宏观经济学和微观经济学的基本概念和原理,从而集中讨论作为地理过程的经济过程.这一问题的特点是地域化,而且要注意的是地理学宏观、微观与经济的宏观、微观完全是两种概念.
我们对地区经济过程的初步理解如下:
(1) 地区内部存在宏观经济过程.地区的宏观经济过程有下面的特点:①地区一般不控制国家银行,不能发行货币;②地区在产品和财政方面与国内其它地区有密切联系,并且受到中央政府的控制或指导;③就业问题及一般人口问题往往在地区政府政策制定中占重要地位.④地区的总需求与总供给是地区宏观经济过程的主要矛盾之一.在宏观经济学中,平衡分析是常用的方法,这方法也适用于分析地理宏观经济过程.
(2) 空间竞争与区位作用是地理学中的主要的经济作用.它们是地理学宏观象,因为它是统计表象.但对经济学来说,产业区位现象是“微观”经济过程.竞争与区位作用具有明显的地理特征,地理学给予特别地重视:
首先,区域与区域间存在竞争,而且竞争往往是不完全竞争.发生不完全竞争的原因是区域总是充填地理空间的,因此区域政府往往有权在管辖范围内制定有利于本区企业和劳动力的政策,有时由于地区文化的影响,消费者可能乐于购买某一地区生产的商品(不一定是本区的),另外不同地区的生产过程也会产生差异产品,这就使得不完全竞争发生.
其次,区域与区域之间存在着区位分异规律和资源、人口、环境约束.区位分异指的是对同一种资源来说,不同区域对它的开发利用中,单位资源量产生的利益不一样,结果空间发生区位分异,使产业向一定地带集中,从而诱发区域分工,再加上资源、人口和环境差异,区域分工更不可避免.
再次,区域生产受到满足本区最低生活需求的诱导,而最大利益原则往往退居第二位.我们认为存在一个“满足本区最低生活需求”的原则,它指的是一个地区的企业往往被民众和政府通过政治的、舆论的和经济的手段,生产出本区缺乏的生活必需品和其它替代品,直到达到满足了人民的最低需求后,企业的生产才能趋向于竞争最大利润.实际上在我国,地区经济结构往往被设计成达到本区的粮食自给.在西方这种需求往往被表现为就业问题.
![]()
廖什区位过程和生产函数描写的地理现象是地理学经济过程的重要形式.关于它们,我们将在第六章详细地考虑.它描述的是经济学所谓的长期均衡现象,以它为代表,地理学重视经济学的长期现象,或许因为它们才有有意义的景观表象.
本文标题:基本地理作用-绪论
手机页面:http://m.dljs.net/dlsk/lidi/21142.html
本文地址:http://www.dljs.net/dlsk/lidi/21142.html

