5．11 空间数据的插值

    从计算机图形角度看，空间的几何形状主要是由自由曲线和曲面组成的。因此，通常可用一组离散的数据点来定义和构造几何形状，这种定义曲线、曲面的方法涉及到插值，逼近拟合，光滑等概念。

    插值——是根据一组已知的数据点，构造一个函数，使已知的数据点全部通过该函数。并用该函数求出其它位置数据点值，这种方法称为插值法，所构造的函数称为插值函数。

    逼近——是根据一组已知的数据点，构造一个函数，使已知的数据点整体上接近该函数，但不必通过全部数据点，但所构成的函数与已知数据点之间的误差在某种意义上值差最小。

    拟合——通常将插值和逼近统称为拟合。

    光滑——光滑是指上面所述的曲线和曲面间具有至少一阶的连续导数。

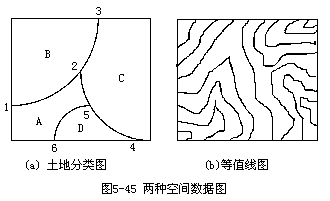
    在地理信息系统中所研究的空间数据是十分复杂且不规则的。它的表现形式可以是具有跳跃特性的离散空间，也可以是具有渐变特点的连续空间。如图5-45(a)所示的土地分类图反映了离散空间，在离散空间的边界上常常有重要的变化，如弧段1，2的上面是B类地，下面是A类地，即土地分类在弧段1，2上发生突变。等值线图反映了连续空间的特性，如图5-37(b)。空间数据的插值就是要寻找一种函数关系式，使它接近或等于已知的空间数据点，并能用该函数求出区域内其它任意点或任意区的数据值。

    空间数据的插值是地理信息系统数据处理和分析的常用方法之一。它在等值线图的自动绘制，数字地面模型的建立，以及区域分析中得到广泛的应用。这里根据所求问题性质的不同分为点插值和区域插值来说明之。

    5．11．1 点插值

    点插值所研究的空间通常是连续空间，所以可采用连续的平滑的数学面加以描述，通常分为整体拟合和局部拟合两大类。整体拟合技术是研究区域内所有采样点上的全部特征值。它一般用于模拟大范围内的变化，即整体趋势面拟合。局部拟合可提供局部区域的内插值，且不受局部范围之外的其他点的影响。

    在地理信息系统中，大量使用局部拟合技术。如为了建立数字高程模型要求出各格网点数据值，或加密格网点时，必须求出未采样点的数值。这些待求数据的确定主要取决于邻近点数据值。

    空间数据的分布是十分复杂的，如地面上的地形是起伏变化的，尤其是丘陵和山区。因此，用一个低次多项式来拟合整个地面形态是不切实际的，而若用高次多项式来模拟又会出现函数的不稳定性。实际上，如果缩小区域的范围，当划分的范围越小，地形变化就越简单，也就越容易拟合。局部插值就是把一定范围的区域分成若干个块，然后利用局部范围内的已知采样点，进行拟合插值的方法。

    有时，为了解决块之间的连接，在相邻块之间可以加适当宽度的重叠带。例如，将100×100m2的分块延伸为140×140m2，即各个方向均延伸20m。用整个扩充范围内的数据来描述整个区域。这时，有效的插值区域仍为100×100m2。延伸的目的是保证各分块之间能比较平滑的连结。这种方法在表达地形变化的数字高程模型的插值中，应用相当广泛。

    1．线性插值。线性插值认为分块区域的形状为一平面，因此，可用线性比例法求得待插值点的值。其函数表达式为：

Zp=a0+a1x+a2y

    使用最靠近待插点的3个已知采样值代入该方程，求出系数a0，a1，a2。从而可求出地理坐标为xp，yp的任意点的Zp值。

    2．双线性多项式插值。双线性多项式插值也称二元一次多项式插值。在这种插值中，待插点的值在与X轴平行的方向上与y成直线比例关系；同样在与Y轴平行的方向上与坐标x成直线比例关系，因此称为双线性插值。其函数表达式为：

Zp=a0+a1x+a2y＋a3xy

    使用最靠近的4个已知采样值代入方程，求出待定系数a0，a1，a2，a3。

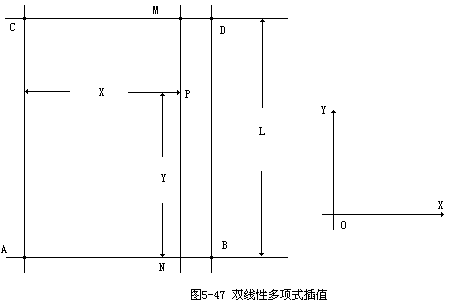
    当4个数据为正方形排列，如图5-47所示，先在A，B和C，D之间进行线性插值求出点M，N的值，再在点M，N间进行线性插值求点P点值。设边长为L，待插点P相对于A点的坐标为X，Y时，则被插点P的值为：

    当选用双线性多项式，进行分块拟合，拼合成的分块逼近面称为二元一次样条曲面。但相邻分片之间会出现些棱边，所以它不完全是光滑的曲面。这种插值方法，在分块中，任一点待插值是根据分块角顶的四个参考点定的。实际上，地表一点的地貌形态，常常与周围的地貌变化相关，因此用邻近参考点数据来计算待插点的值较为合理。双线性插值的优点是具有保凸性和逼真性，但它所拟合的曲面不够光滑。

    3．双三次多项式(样条函数)插值。双三次多项式插值，将每个分块拟合成双三次多项式。此外，在相邻分块的连接处的X轴和Y轴方向上斜率都保持连续，相邻分块连接处的扭矩连续。拼接后整个分块的逼近面称为二元三次样条曲面。其函数表达式为：

    Z=f(x，y)=a1x3y3+a2x2y3+a3xy3+a4y3+a5x3y2+a6x2y2+a7xy2

+a8y2+a9x3y+a10x2y+a11xy+a12x3+a14x2+a15x+a16 (5-6)

    设分块范围内的数据点按单位边长正方形格网排列，每分块是一个单位边长正方形如图5-48所示，取分块左下角点为坐标原点。由于每个分块单元仅有4个格网信息值，而函数待定系数为16个，为此用数据点

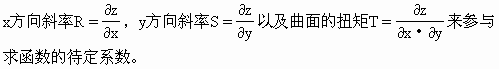
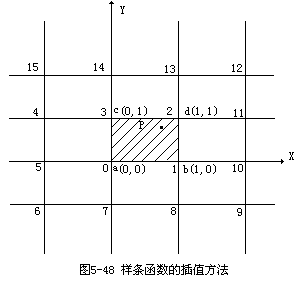
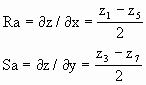
    同理得：

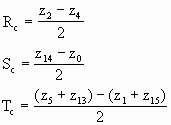
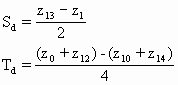
    因此，以4个数据点a(0，0)，b(1，0)，c(0，1)，d(1，1)代入式5-6，可列出Z，R，S，T的关系式为：

    写成矩阵形式Z=K·A，从而可求出函数的16个待定系数A=K-1Z。因此，对于分块中任意点P，把它的平面直角坐标(Xp，YP)代入，即可求出其值。

    如果在格网abcd内内插n×n个正方形，即加密格网，则需要将式

    这是一种典型的逐点内插法。这种方法以待定点为中心进行内插，也就是内插时，先作坐标变换，将平面坐标的原点移到内插点。

    当待定点成为平面坐标的原点后，移面是以待定点为形心，用适当半径的圆或适当边长的正方形区域内的全部或部分数据点求得数学面，其数学模型可以是前一节所述的一次平面或二次多项式，也可以取加权平均。但考虑到表面的光滑性，常用二次曲面。二次多项式函数为：

Zp=a1x2+a2xy+a3y2+a4x+a5y+a6

    该函数有6个待求参数，因此，取6个采样数据代入即可求出。

    当移面内采样点数大于6个时，可将距离较远的参考点去除，当采样点数小于6时，可扩大移面范围。

    考虑到数据圆中各点对中心点的作用不同，可加权重值。如可认为距内插点越近的点，对待求点值的影响越大，当内插点无限接近某一采样数据点时，则该数据点的权应为无穷大。假设di为采样点和待求点间距离，通常可采用的加权形式为：

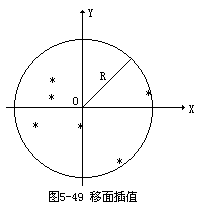
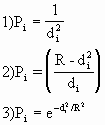
    在用单点移面内插时，若移面内出现突变，如图5-50所示，在移面内有山谷线穿过时，用加权法不能有效逼近，有时距离权重的引入，很可能进一步损坏内插的精度。如图5-50所示的A点，它离P点距离远比B，C点离P点距离为近，然而A点在山谷线的另一侧坡面上，但该点不能用距离加权法参予运算。因此，在进行单点移面内插时，最好判断一下移面内有否突变，如地性线。若移面内含有地性线，应按地性线再分割，直到不含地性线为止。

    5．11．2 区域插值

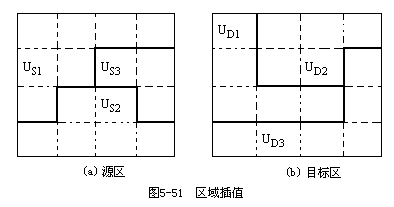
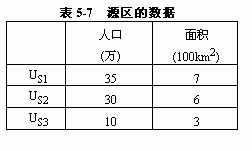
    点插值主要用于解决对连续空间数据的插值。实际上，空间数据中存在着大量离散空间数据。例如，很多以区域为单位的社会经济数据，如人口统计数据，国民经济产值数据等。图5-51(a)表示了一地区3个不同分区的人口统计值，该区的面积和人口统计数据见表5-7。现在要求出图5-51(b)所示的区域中的人口数。解决这类问题不能用前面所述的插值方法，而需要用区域插值法。区域插值是研究从一组已知的分区数据中推断出同一地区的另一组分区数据的插值方法。

    叠合法的前提是认为在源区和目标区内数据是均匀分布的。求解时，将目标区叠合到源区上，求出源区和目标区之间的交集。

    目标区内各分区的数据按如下公式计算：

    其中：UDi为目标区第i分区的值，i=1，2……m；

    Usj为源区第j个分区的值，j=1，2……n；

    aDj为第i个目标分区同有第j个源区的面积比。

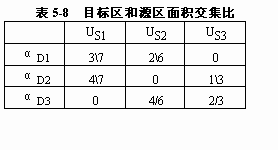
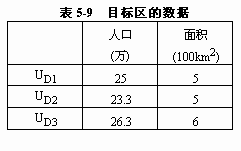
    例如，图5-51 将目标区和源区叠合得到表5-8。从表5-8可知，目标区D1的面积是由3/7的Usi区面积和2/6的US2区的面积组成的。如果源区和目标区内各分区人口分布密度相同，按上式，就可算出目标区各分区的人口，并列于表5-9中。其中：

    UD1=35×3/7+30×2/6=25

    UD2=35×4/7+10×1/3=23.3

    UD3=30×4/6+10×2/3=26.6

    以上是已知源分区的统计值，如总人口，总产值求同一地区目标分区的统计值。同样可以从已知源分区的密度数据，如人口密度，求出同一区域内目标分区的密度数据。同理，可以从已知源分区的比值数据，如农业产值占国民经济总产值比，求出同一区域内目标分区的比值数据。

    上述叠合法进行区域插值时，认为源和目标区内的数据是均匀同质的。比重法是根据平滑密度函数原理，将源区的统计数据从同质性改变成非同质性，然后进行区域插值。现实中，很多社会经济数据在一个分区内其分布密度或规律往往是不均匀的，因此这种算法更符合实际。其算法过程如下：

    1．在源区上叠置一网格，网格的尺寸应选择确保有足够内插精度。

    2．将源区中各分区的内各栅格赋予平均值如图5-53(a)所示。再以四邻域法或八邻域法求出各区栅格点的值。四邻域的平均值Zp=(Zi，j+1+Zi，j-1+Zi-1，j+Zi+1，j)/4，八邻域的平均值Zp=(Zi，j+1＋Zi，j-1＋Zi-1，j＋Zi+1，j+Zi+1，j+1＋Zi+1，j-1＋Zi-1，j+1＋Zi-1，j-1)/8

    这里将图5-53(a)中各网格数据用八邻域法平滑得数据如图5-53(b)所示。

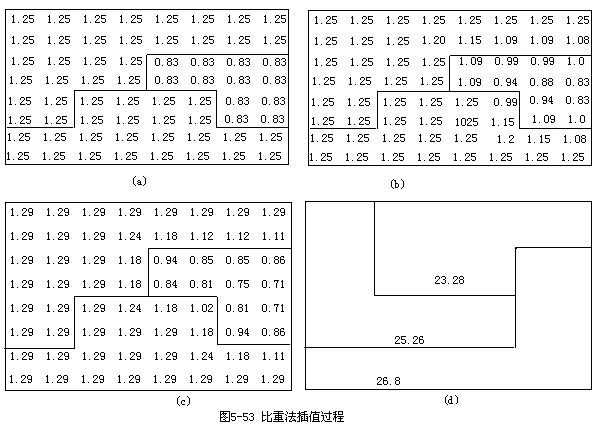
    3．将四邻域(或八邻域)的平均值以分区为单位相加，得值为Usi′，求出各分区系数ei=Usi/Usi′，由图 5-53(b)求出e1=35/34.16=1.03，e2=30/29.17=1.03，e3=10/11.67=0.86。并将图5-53(b)中各栅格点的值乘以相应分区的系数ei，得图5-53(c)。不断循环2， 3步，直到ei值接近1为止。本例中图5-53(c)，所求得分区系数分别为：

    e2=30/30.08=0.997

    e3=10/10.01=0.999

    满足ei＞0.99要求，不再循环计算。

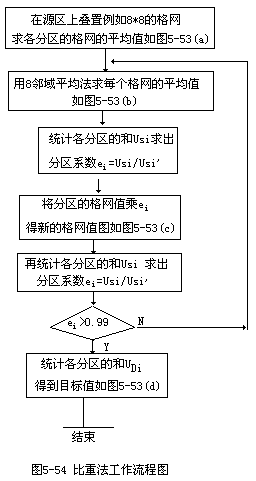
    4．计算目标分区值。利用源区的非同质数据的结果，计算目标分区值，得图5-53(d)所示结果。图5-54为用比重法对上述数据进行区域插值的流程图。